例14. (コ)ホモロジー(加)群

まず，数学を理解することについてを読んでください。以下もその例です。
今回の話は，例7, 例8, 例9, 例10, 例13の続きです。もちろん例11, 例12とも関係します。

例10では，まず環 $R$ と$R$-加群と加群の間の準同型について注意したあと，
(まだ慣れていない場合，環 $R$ を体あるいは $\mathbb{Z}$ として，$R$-加群といえば，それぞれベクトル空間あるいはアーベル群と思い， $R$-加群の間の準同型といえば，それぞれベクトル空間の間の線形写像あるいはアーベル群の間の準同型と思って読んでください。)
加群と準同型からなる，完全列の定義を導入し，それを絵に描きました。

　次に，複体のホモロジー加群（余複体のコホモロジー加群）について話そうと思います。これを考える動機を述べるために，前回の例13では，圏と関手について説明しておきました。

完全列の半分の条件.

前回の復習で，もう一度完全列を考えます。$R$-加群とその間の準同型の列

$X_1 \xrightarrow{f_1} X_2 \xrightarrow{f_2} \cdots \xrightarrow{f_{n-1}} X_n$

($n \ge 3$) が完全であるとは，すべての $i=1, 2, \ldots, n-1$ に対して，

$\mathrm{Im}\, f_i = \mathrm{Ker}\, f_{i+1}$

が成り立つことでした。この条件は2つに分けることができます。

$\mathrm{Im}\, f_i \subseteq \mathrm{Ker}\, f_{i+1} \tag{a}$

$\mathrm{Im}\, f_i \supseteq \mathrm{Ker}\, f_{i+1} \tag{b}$

これらのうち (a) は，次と同値でした：

$f_{i+1} f_{i} = 0$

ここで，上で考えた $\mathbb{Z}$-関手 $F:= \mathrm{Hom}_R(X, ?)$ を上の列に作用させると，圏 $\mathrm{Mod}\, \mathbb{Z}$ における列

$F(X_1) \xrightarrow{F(f_1)} F(X_2) \xrightarrow{F(f_2)} \cdots \xrightarrow{F(f_{n-1})} F(X_n)$

が得られ， $F$ が合成の保存性と和の保存性をもっていることから

$F(f_{i+1})F(f_{i}) = 0$

が得られたのでした。これより，

$\mathrm{Im}\, F(f_i) \subseteq \mathrm{Ker}\, F(f_{i+1})$

が成り立ちます。（しかしこの逆は成り立つとは限りません。そのような例も，前回与えておきました。）
　このように完全列の性質のうちの半分は，$\mathbb{Z}$-関手で保たれるものです。この性質をもつ列を複体とよびます。上では有限の準同型からなる列しか考えていませんでしたが，複体を考えるときは（左右に）無限の列を考えます。

定義 1. $R$-加群とその間の準同型からなる列 $X_{\centerdot}$

 $\cdots\xrightarrow{d_{i+2}} X_{i+1} \xrightarrow{d_{i+1}} X_{i} \xrightarrow{d_{i}} \cdots X_2 \xrightarrow{d_2} X_1 \xrightarrow{d_1} \cdots$

は，どの $i \in \mathbb{Z}$ に対しても $d_i d_{i+1} = 0$ をみたすとき，複体とよばれる。

$B_i:= B_i(X_{\centerdot}):= \mathrm{Im}\, d_{i+1}$, $Z_i:=Z_i(X_{\centerdot}):=\mathrm{Ker}\, d_i$ とおきます。 $B_i$ の元を $X_{\centerdot}$ の $i$ 次境界輪体 (boundary)，$B_i$ を $X_{\centerdot}$ の $i$ 次境界輪体加群，$Z_i$ の元を $X_{\centerdot}$ の $i$ 次輪体 (cycle) ，$Z_i$ を $X_{\centerdot}$ の $i$ 次輪体加群 とよびます。条件 $d_i d_{i+1} = 0$ は，

$B_i \subseteq Z_i$

と同値です。
上のように，添字を下に付けるときは，番号を左から右へ小さくしていく習慣があります。番号を左から右へ大きくしていくときは，添字を上に付けることになっています：

定義 1'. $R$-加群とその間の準同型からなる列 $X^{\centerdot}$

 $\cdots \xrightarrow{d^0} X^1 \xrightarrow{d^1} X^2 \xrightarrow{d^2} \cdots X^{i-1} \xrightarrow{d^{i-1}} X^{i} \xrightarrow{d^{i}} \cdots$

は，どの $i \in \mathbb{Z}$ に対しても $d^{i} d^{i-1} = 0$ をみたすとき，余複体とよばれる。

$B^i:=B^i(X^{\centerdot}):= \mathrm{Im}\, d^{i-1}$, $Z^i:=Z^i(X^{\centerdot}):=\mathrm{Ker}\, d^i$ とおきます。$B^i$ の元を $X^{\centerdot}$ の $i$ 次余境界輪体 (coboundary)，$B^i$ を $X^{\centerdot}$ の $i$ 次余境界輪体加群，$Z^i$ の元を $X^{\centerdot}$ の $i$ 次余輪体 (cocycle) ，$Z^i$ を $X^{\centerdot}$ の $i$ 次余輪体加群 とよびます。条件 $d^{i} d^{i-1} = 0$ は，

$B^i \subseteq Z^i$

と同値です。

複体を絵で描いておきます。まず，ベクトル空間の場合。

次に一般の場合

上の説明から次は明らかでしょう。

命題. $\mathbb{Z}$-関手は複体を複体に移す。

定義 2. $X_{\centerdot}$ を複体とし， $i \in \mathbb{Z}$ とする。 $H_i(X_{\centerdot}):= Z_i/B_i$ を $X_{\centerdot}$ の $i$ 次ホモロジー加群とよぶ。

定義 2'.  $X^{\centerdot}$ を余複体とし， $i \in \mathbb{Z}$ とする。 $H_i(X^{\centerdot}):= Z^i/B^i$ を $X^{\centerdot}$ の $i$ 次コホモロジー加群とよぶ。

大まかにいうと，（余）複体の（コ）ホモロジー加群というのは，その（余）複体がどれぐらい完全列であることから離れているかを測るものです。（コ）ホモロジー加群がすべての次数で0であることが，列として完全列であるということです。完全列であるような複体を
非輪状 (acyclic) 複体といいます。

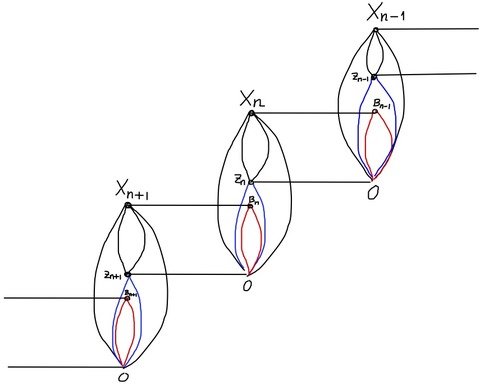
ホモロジー加群の絵を描いておきます。まずベクトル空間の場合。

次に一般の場合，